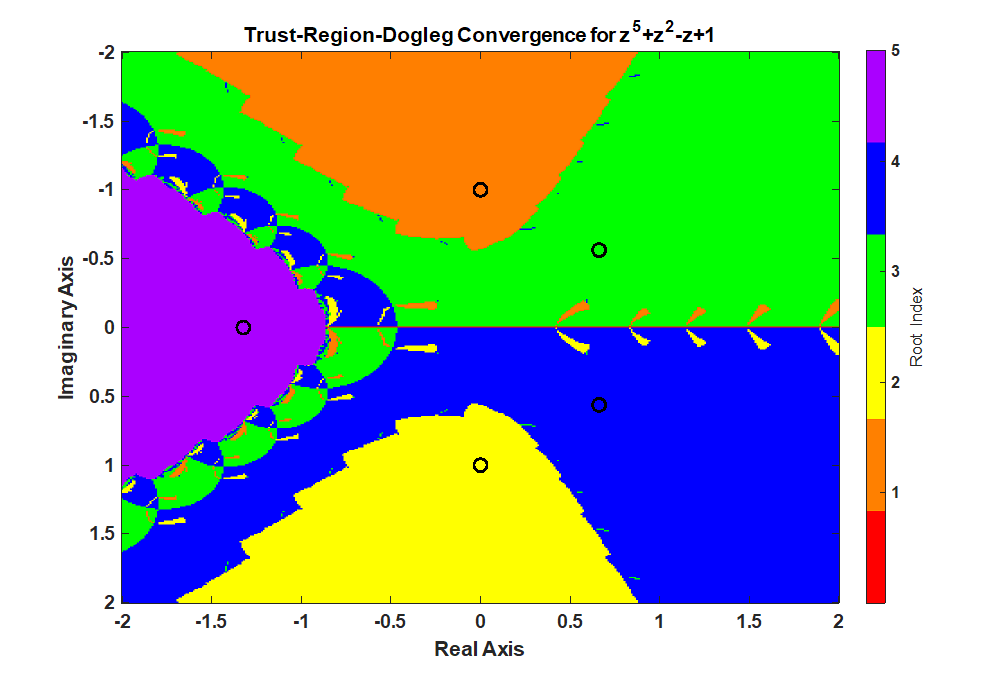
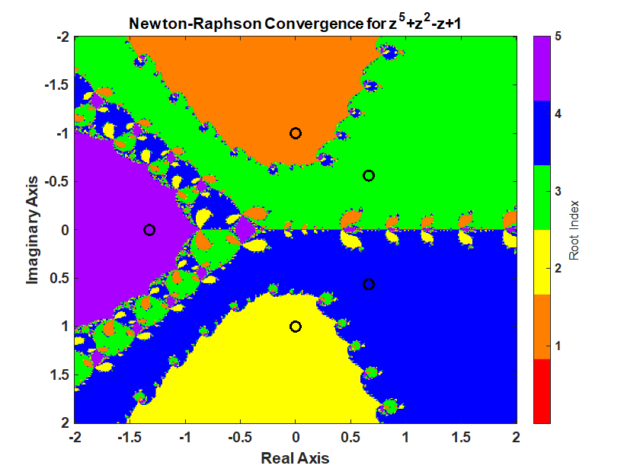
A Newton-Raphson iteration produces a fractal pattern in the complex plane and a Trust-Region-Dogleg method produces a smoother pattern in the complex which is desirable for a nonlinear equation solver. The context of this statement is finding the roots of a polynomial in a complex plan from different starting points. The inspiration for this post was the video from 3Blue1Brown, Newton’s Fractal (which Newton knew nothing about).
clc;clear; close all;
Given the polynomial
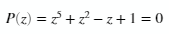
find a root starting from anywhere in the interval of -2 to 2 and -2i to 2i.
common code
% setup polynomial function coefficients = [1 0 0 1 -1 1]; polynomialFunction = @(z) polyval(coefficients, z); % setup the derivative of the polynomial function coefficients_dot = polyder(coefficients); polynomialDerivativeFunction = @(z) polyval(coefficients_dot, z); % roots of the polynomial. roots uses a eigenvalues of a companion matrix approach. % rootsOfPolynomial = roots(coefficients); % exact roots rootsOfPolynomial(1) = -1i; rootsOfPolynomial(2) = 1i; rootsOfPolynomial(3) = (2^(2/3)*(3^(1/3) - 3^(5/6)*1i)*(69^(1/2) + 9)^(1/3))/12 + (2^(2/3)*3^(1/3)*(9 - 69^(1/2))^(1/3))/12 + (2^(2/3)*3^(5/6)*(9 - 69^(1/2))^(1/3)*1i)/12; rootsOfPolynomial(4) = (2^(2/3)*(3^(1/3) + 3^(5/6)*1i)*(69^(1/2) + 9)^(1/3))/12 + (2^(2/3)*3^(1/3)*(9 - 69^(1/2))^(1/3))/12 - (2^(2/3)*3^(5/6)*(9 - 69^(1/2))^(1/3)*1i)/12; rootsOfPolynomial(5) = -(2^(2/3)*3^(1/3)*((69^(1/2) + 9)^(1/3) + (9 - 69^(1/2))^(1/3)))/6; % Calculate a grid of starting points using the ndgrid format. x (real part) % follow rows (1st dimension) and y follows the columns (2nd dimension). % ndgrid is format is transpose of meshgrid format. meshgrid format is used % for plotting surfaces. nStartingPointReal = 400; nStartingPointImaginary = 401; startingPointReal = linspace(-2,2,nStartingPointReal)'; startingPointImaginary = linspace(-2,2+eps(2),nStartingPointImaginary)*1i; startingPoint = startingPointReal + startingPointImaginary; % using singleton expansion maxIterations = 100; functionTolerance = 1e-14; divideByZeroTolerance = 1000; % 1000*eps(p)
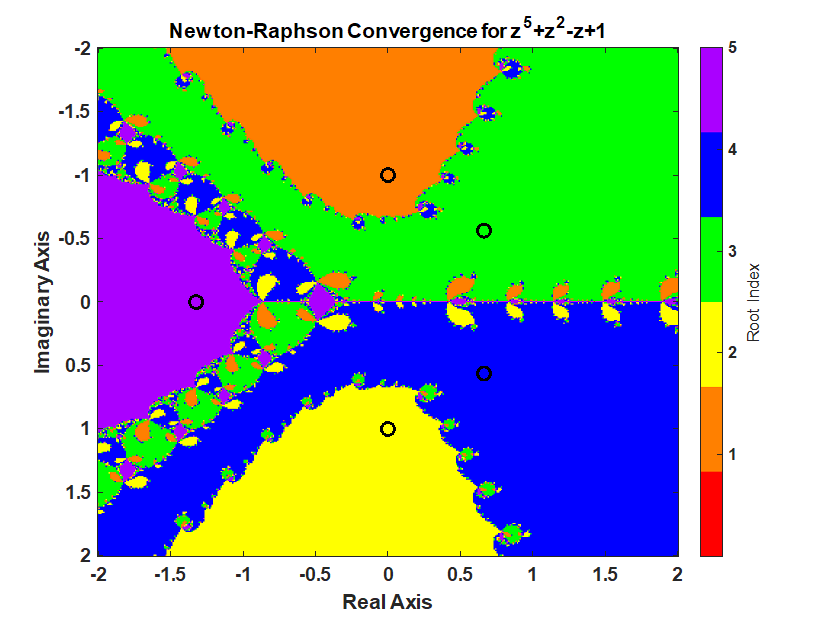
Newton-Raphson Iteration
Using Newton’s method starting anywhere in the interval -2 to 2 and -2i to 2i produces the following pattern.
% setup for iteration isConverged = false(nStartingPointReal, nStartingPointImaginary); isDivideByZero = false(nStartingPointReal, nStartingPointImaginary); whileFlag = true; iteration = 0; z = startingPoint; % check if the starting value was already converged. % polynomial is less then functionTolerance. p = polynomialFunction(z(~isConverged)); isConverged(~isConverged) = abs(p) < functionTolerance; % begin iteration p = polynomialFunction(z(~isConverged)); while whileFlag % increment iteration number iteration = iteration + 1; p = polynomialFunction(z(~isConverged)); % Calculate the derivative of the polynomial. % Check for divide by 0. If p_dot is close to machine precision % of p, then its a divide by 0 error. % Stop all further iteration. p_dot = polynomialDerivativeFunction(z(~isConverged)); isDivideByZeroIteration = abs(p_dot) < divideByZeroTolerance*eps(abs(p)); isDivideByZero(~isConverged) = isDivideByZeroIteration; isConverged(~isConverged) = isDivideByZeroIteration; % calculate Newton iteration on unconverged points. z(~isConverged) = z(~isConverged) - p(~isDivideByZeroIteration)./p_dot(~isDivideByZeroIteration); % check for convergence p = polynomialFunction(z(~isConverged)); isConverged(~isConverged) = abs(p) < functionTolerance; % set while flag % all roots have converged or reached max iterations whileFlag = iteration <= maxIterations || all(all(~isConverged)); end % successful roots isRoot = isConverged & ~isDivideByZero; % which root did newton's method converge too? % calculate the difference between the converged root and the roots of the polynomial % the smallest distance corresponds to the root index zDiff = abs(z - reshape(rootsOfPolynomial,1,1,[])); % using singelton expansion [rootErrors,rootIndex] = min(zDiff,[],3); % minimum along 3rd dimension rootIndex(~isRoot) = 0; % create the fractal image % imagesc uses the meshgrid format where % x is the 2nd dimension % y is the first dimension % therefore, transpose rootIndex because its in the ndgrid format figure; imagesc(startingPointReal', imag(startingPointImaginary), rootIndex') c = prism(numel(rootsOfPolynomial)+1); colormap(c); xlabel("Real Axis"); ylabel("Imaginary Axis") ylabel(colorbar('Ticks',1:numel(rootsOfPolynomial)),"Root Index") hold all; plot(rootsOfPolynomial,'ko','MarkerSize',10,'LineWidth',3) title("Newton-Raphson Convergence for z^5+z^2-z+1")
Trust-Region-Dogleg Iteration
The MATLAB fsolve() function uses the Trust-Region-Dogleg method to find a root of a nonlinear equation. What’s interesting is how much smoother the boundaries are for the Trust-Region-Dogleg method.
More information on Trust-Region-Dogleg method
Powell’s dog leg method – Wikipedia
Trust-Region-Dogleg Algorithm – MathWorks
options = optimoptions('fsolve','Display',"none","SpecifyObjectiveGradient",true, ... 'FunctionTolerance',functionTolerance, 'StepTolerance',max(rootErrors(isRoot)),... "Algorithm","trust-region-dogleg"); % calling fsolve with the first argument as a cell array is undocumented but it works and is easy to setup. In a future % version of MATLAB, this may not work because its undocumented. Also, each root is found one at a time and this is % ver inefficient. This could be a lot better but that is not the focus of today. % tic; [z2,~,exitflag2] = arrayfun(@(z0) fsolve({polynomialFunction,polynomialDerivativeFunction},z0,options),startingPoint); toc;
Elapsed time is 406.891834 seconds.
% successful roots isRoot2 = exitflag2 == 1; % which root did the Trust-Region-Dogleg method converge too? % calculate the difference between the converged root and the roots of the polynomial % the smallest distance corresponds to the root index zDiff2 = abs(z2 - reshape(rootsOfPolynomial,1,1,[])); % using singelton expansion [rootErrors2,rootIndex2] = min(zDiff2,[],3); % minimum along 3rd dimension rootIndex2(~isRoot2) = 0; % create the fractal image % imagesc uses the meshgrid format where % x is the 2nd dimension % y is the first dimension % therefore, transpose rootIndex2 because its in the ndgrid format figure; imagesc(startingPointReal', imag(startingPointImaginary), rootIndex2') colormap(c); xlabel("Real Axis"); ylabel("Imaginary Axis") ylabel(colorbar('Ticks',1:numel(rootsOfPolynomial)),"Root Index") hold all; plot(rootsOfPolynomial,'ko','MarkerSize',10,'LineWidth',3) title("Trust-Region-Dogleg Convergence for z^5+z^2-z+1")